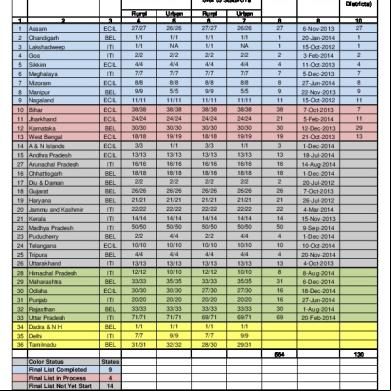
1g Increase In Draft Due To List 5b1f2q

INCREASE IN DRAUGHT DUE TO LIST For box-shaped vessels : Draught is defined as the vertical distance between the keel and the waterline, measured either forward, aft or amidships in metres. Consider a box-shaped vessel floating upright on an even keel with draught “ d ” having beam “ b ”.

b

O

A

d

B K

Now consider the same vessel listed to an angle Ө. The new increased draft on the listed side is “D”. It is seen; D = AX + AY In triangle AOX ,

Sin Ө = AX/OA

So AX = OA Sin Ө, but

OA = ½ b (breadth)

therefore AX = ½ b Sin Ө , similarly AY = d Cos Ө Thus Increased draft, D = ½ b Sin Ө + d Cos Ө b

O

Ө

X Ө A d Ө

K B

Y

D

For Ship Shape Vessels : For vessels with a rise of floor the formula can be further modified as follows;

New draft in listed / heeled condition,

D = ½ b Sin Ө + (d - Rise of floor) Cos Ө

Where b = beam of vessel d = draft in upright condition

Note : The rise of floor is assumed to be linear

The sketch and example on the following page will make things clearer.

Example 1 (box shaped vessels) A box-shaped ship with 12 m. beam is floating upright at a draft of 6.7m. Find the increase in draft if the vessel is now listed 18 degrees.

Figure 1(c).

From Previous : AX = 1/2 beam x Sin List = 1/2 x 6 x Sin 18 = 1.85m AY = Old draft x Cos List = 6 x Cos 18 = 6.37m New Draft - XY = 8.23 m Increase in draft = 8.23 - 6.7 = 1.526 m

Example 2 (Vessels having a rise of floor) A ship has 20 m. beam at the waterline and is floating upright at 6 m. draft. If the rise of floor is 0.25 m., calculate the new draft if the ship is now listed 15 degrees. (See Figure 1(d), below)

Fig. 1 (d) The formula is modified form of previous and is given by : New Draft = 1/2 beam x Sin List + (Old draft - Rise of floor) Cos List. = 1/2 x ( 20 x Sin 15 ) + (Old Draft -Rise of floor) Cos List = 1/2 x ( 5.176) + ( 6 - 0.25 ) Cos 15 = 2.588 + 5.555 = 8.14 metres Ans.