Modelo Clásico De Series De Tiempo 316q26
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3i3n4
Overview 26281t
& View Modelo Clásico De Series De Tiempo as PDF for free.
More details 6y5l6z
- Words: 1,226
- Pages: 19
CLÁSICO DE SERIES DE TIEMPO ESTADISTICA INFERENCIAL II 41V INGENIERIA INDUSTRIAL • GUTIERREZ CASTELLANOS VICENTE • MENDIOLA SOTELO OSCAR DAMIAN • VARGAS TORRES LAURA YURITZI
SERIES DE TIEMPO En Estadística se le llama así a un conjunto de valores observados durante una serie de períodos temporales secuencialmente ordenada, tales períodos pueden ser semanales, mensuales, trimestrales o anuales. Una serie de tiempo es un conjunto de valores numéricos obtenidos en periodos iguales en el tiempo
Por serie de tiempo nos referimos a datos estadísticos que se recopilan, observan o registran en intervalos de tiempo regulares (diario, semanal, semestral, anual, entre otros). El término serie de tiempo se aplica por ejemplo a datos registrados en forma periódica que muestran, por ejemplo, las ventas anuales totales de almacenes, el valor trimestral total de contratos de construcción otorgados, el valor trimestral del PIB.
OBJETIVO La suposición fundamental del análisis de series de tiempo es que los factores que han influido en los patrones de actividad en el pasado y el presente tendrán más o menos la misma influencia en lo futuro Analizar una serie de tiempo tiene como objetivos, entre otros:
Determinar si se presentan ciertos patrones o pautas no aleatorias
Aislar y entonces estudiar sus componentes a fin de proporcionar claves para movimientos futuros.
Hace posible pronosticar los movimientos futuros así como otros aspectos que estén sincronizados.
EJEMPLO GRÁFICOS DE SERIES DE TIEMPO
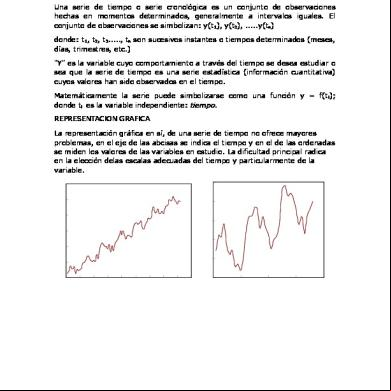
Se representa por medio de una gráfica de líneas sobre cuyo eje horizontal se representan los períodos y en cuyo eje vertical se representan los valores de la serie de tiempo.
Para
CARACTERISTICAS
llevar a cabo un análisis de este tipo, primero se deben identificar los componentes de la serie de tiempo, después aplicar las técnicas estadísticas para su análisis y, finalmente, hacer las proyecciones o pronósticos de eventos futuros.
De
esta forma, el análisis de series de tiempo es el procedimiento por el cual se identifican y aíslan los factores relacionados con el tiempo que influyen en los valores observados en las series de tiempo para que una vez identificados ,estos factores puedan contribuir a la interpretación de valores históricos de series de tiempo y hasta entonces pronosticar valores futuros de series de tiempo.
COMPONENTES DE LA SERIES DE TIEMPOS
El método clásico identifica cuatro influencias o componentes: •
Tendencia (T)
•
Fluctuaciones cíclicas (C)
•
Variaciones estacionales (E)
•
Variaciones irregulares (I)
Los cuales tienen una relación multiplicativa que dan forma al modelo clásico de series de tiempo, es decir, para cualquier período designado en la serie de tiempo, el valor de la variable está determinado por los cuatro componentes en la siguiente forma:
TENDENCIA (T) Es el movimiento general a largo plazo de los valores de la serie de tiempo (y) sobre un extenso periodo de años. Son tendencias a largo plazo de ventas, empleo, el precio de las acciones, y otras series económicas y comerciales (sin alteraciones de una serie de tiempo). El movimiento secular presenta movimientos suaves de largo plazo, los cuales están dominados por factores de tipo económico.
Ventas a largo plazo, ofertas de empleo, precios de secciones son ejemplos de tendencia secular. Se miden en años, algunas se mueven continuamente hacia arriba, otras declinan, otras mas permanecen sin cambio en cierto periodo.
FLUCTUACIONES CÍCLICAS (C)
Movimientos ascendentes y descendentes recurrentes respecto a la tendencia con una duración de años. Es el ascenso y descenso de una serie de tiempo en periodos mayores a un año. El componente cíclico es la fluctuación en forma de onda alrededor de la tendencia, por lo que afecta regularmente las condiciones
• Empleo, la producción, el precio de las acciones, son ejemplos de fluctuaciones cíclicas. • Se miden en años. • Representan ascenso y descenso en periodos mayores de un año. • Sufren de un periodo de prosperidad seguidos de recesión, depresión y luego recuperación.
VARIACIONES Movimientos ascendentes y descendentes respecto a la ESTACIONALES (E) tendencia que se consuman dentro de un año y se repiten anualmente.
El componente estacional se refiere a un patrón de cambio que se repite a si mismo año tras año. En el caso de series mensuales, el componente estacional mide la variabilidad de las series, por ejemplo, de enero, febrero, etc. En las series trimestrales hay cuatro elementos estaciónales, uno para cada trimestre.
Ventas altas en navidad y bajas después, Consumos relacionados con las estaciones del año son ejemplos de variaciones estacionales. Solo se aprecian si se tienen datos trimestrales o mensuales. En de Patrones de observa un mismoningún año, tales que el cambio gráficodentro no se movimiento se repiten cada año. estacional, puesto que se trata de una serie anual.
VARIACIONES IRREGULARES Variaciones erráticas respecto de la (I) tendencia que no pueden atribuirse a influencias cíclicas o estacionales.
El componente aleatorio mide la variabilidad de las series de tiempo después de que se retiran los otros componentes. Contabiliza la variabilidad aleatoria en una serie de tiempo ocasionada por factores imprevistos y no ocurrentes. La mayoría de los componentes irregulares se conforman de variabilidad aleatoria, si embargo, los sucesos impredecibles pueden provocar irregularidad en una variable.
Guerras, Huelgas y Desastres Naturales son ejemplos de variaciones irregulares. Estas variaciones se pueden predecir y medir pero no con certeza.
MODELO DE SERIES DE Se llama Serie de Tiempo, a un conjunto de mediciones de ciertoTIEMPO fenómeno o experimento registradas secuencialmente en el tiempo, por ejemplo a cada hora,
mensualmente, trimestralmente, semestralmente, etc.. Series de tiempo discreto, equiespaciadas en cuyo caso se asume que: {x(t1), x(t2), ..., x(tn)}= {x(1), x(2), ..., x(n)}. Debido al carácter introductorio se restringió al caso de series de tiempo univariadas. Al analizar una serie de tiempo, lo primero que se debe hacer es graficar la serie. Esto nos permite detectar las componentes esenciales de la serie. El gráfico de la serie permitirá: detectar Outlier, detectar tendencias, variación estacional, variaciones irregulares (o componente aleatoria).
Un modelo clásico para una serie de tiempo, puede ser expresada como suma o producto de tres componentes: tendencia, estacional y un término de error aleatorio. Existen tres modelos de series de tiempos. Estos son: 1.Aditivo: X(t) = T(t) + E(t) + A(t) 2.Multiplicativo: X(t) = T(t) · E(t) · A(t) 3.Mixto: X(t) = T(t) · E(t) + A(t)
Con el fin de obtener un modelo, es necesario estimar la tendencia y la estacionalidad. Para estimar la tendencia, se supone que la componente estacional no está presente. La estimación se logra al ajustar a una función de tiempo a un polinomio o suaviza miento de la serie a través de los promedios móviles. Para estimar la estacionalidad se requiere haber decidido el modelo a utilizar
APLICACIÓN Las series de tiempo se pueden citar en distintas áreas: Series económicas Series físicas Geofísica
Series de tiempo
Series demográficas Series de marketing Series de telecomunicación Series de transporte
EJEMPLOS DE LA APLICACIÓN
SERIES DE TIEMPO 1. Series económicas: 2. Series Físicas: 3. Geofísica: 4. Series demográficas: 5. Series de marketing: 6. Series telecomunicación: 7. Series de transporte:
EJEMPLOS
-
Precios de un artículo Tasas de desempleo Tasa de inflación Índice de precios, etc. Meteorología Cantidad de agua caída Temperatura máxima diaria Velocidad del viento (energía eólica) Energía solar, etc. Series sismologías
Tasas de crecimiento de la población Tasa de natalidad, mortalidad Resultados de censos poblacionales
- Series de demanda, gastos, ofertas de - Análisis de señales - Series de tráfico
SERIES DE TIEMPO En Estadística se le llama así a un conjunto de valores observados durante una serie de períodos temporales secuencialmente ordenada, tales períodos pueden ser semanales, mensuales, trimestrales o anuales. Una serie de tiempo es un conjunto de valores numéricos obtenidos en periodos iguales en el tiempo
Por serie de tiempo nos referimos a datos estadísticos que se recopilan, observan o registran en intervalos de tiempo regulares (diario, semanal, semestral, anual, entre otros). El término serie de tiempo se aplica por ejemplo a datos registrados en forma periódica que muestran, por ejemplo, las ventas anuales totales de almacenes, el valor trimestral total de contratos de construcción otorgados, el valor trimestral del PIB.
OBJETIVO La suposición fundamental del análisis de series de tiempo es que los factores que han influido en los patrones de actividad en el pasado y el presente tendrán más o menos la misma influencia en lo futuro Analizar una serie de tiempo tiene como objetivos, entre otros:
Determinar si se presentan ciertos patrones o pautas no aleatorias
Aislar y entonces estudiar sus componentes a fin de proporcionar claves para movimientos futuros.
Hace posible pronosticar los movimientos futuros así como otros aspectos que estén sincronizados.
EJEMPLO GRÁFICOS DE SERIES DE TIEMPO
Se representa por medio de una gráfica de líneas sobre cuyo eje horizontal se representan los períodos y en cuyo eje vertical se representan los valores de la serie de tiempo.
Para
CARACTERISTICAS
llevar a cabo un análisis de este tipo, primero se deben identificar los componentes de la serie de tiempo, después aplicar las técnicas estadísticas para su análisis y, finalmente, hacer las proyecciones o pronósticos de eventos futuros.
De
esta forma, el análisis de series de tiempo es el procedimiento por el cual se identifican y aíslan los factores relacionados con el tiempo que influyen en los valores observados en las series de tiempo para que una vez identificados ,estos factores puedan contribuir a la interpretación de valores históricos de series de tiempo y hasta entonces pronosticar valores futuros de series de tiempo.
COMPONENTES DE LA SERIES DE TIEMPOS
El método clásico identifica cuatro influencias o componentes: •
Tendencia (T)
•
Fluctuaciones cíclicas (C)
•
Variaciones estacionales (E)
•
Variaciones irregulares (I)
Los cuales tienen una relación multiplicativa que dan forma al modelo clásico de series de tiempo, es decir, para cualquier período designado en la serie de tiempo, el valor de la variable está determinado por los cuatro componentes en la siguiente forma:
TENDENCIA (T) Es el movimiento general a largo plazo de los valores de la serie de tiempo (y) sobre un extenso periodo de años. Son tendencias a largo plazo de ventas, empleo, el precio de las acciones, y otras series económicas y comerciales (sin alteraciones de una serie de tiempo). El movimiento secular presenta movimientos suaves de largo plazo, los cuales están dominados por factores de tipo económico.
Ventas a largo plazo, ofertas de empleo, precios de secciones son ejemplos de tendencia secular. Se miden en años, algunas se mueven continuamente hacia arriba, otras declinan, otras mas permanecen sin cambio en cierto periodo.
FLUCTUACIONES CÍCLICAS (C)
Movimientos ascendentes y descendentes recurrentes respecto a la tendencia con una duración de años. Es el ascenso y descenso de una serie de tiempo en periodos mayores a un año. El componente cíclico es la fluctuación en forma de onda alrededor de la tendencia, por lo que afecta regularmente las condiciones
• Empleo, la producción, el precio de las acciones, son ejemplos de fluctuaciones cíclicas. • Se miden en años. • Representan ascenso y descenso en periodos mayores de un año. • Sufren de un periodo de prosperidad seguidos de recesión, depresión y luego recuperación.
VARIACIONES Movimientos ascendentes y descendentes respecto a la ESTACIONALES (E) tendencia que se consuman dentro de un año y se repiten anualmente.
El componente estacional se refiere a un patrón de cambio que se repite a si mismo año tras año. En el caso de series mensuales, el componente estacional mide la variabilidad de las series, por ejemplo, de enero, febrero, etc. En las series trimestrales hay cuatro elementos estaciónales, uno para cada trimestre.
Ventas altas en navidad y bajas después, Consumos relacionados con las estaciones del año son ejemplos de variaciones estacionales. Solo se aprecian si se tienen datos trimestrales o mensuales. En de Patrones de observa un mismoningún año, tales que el cambio gráficodentro no se movimiento se repiten cada año. estacional, puesto que se trata de una serie anual.
VARIACIONES IRREGULARES Variaciones erráticas respecto de la (I) tendencia que no pueden atribuirse a influencias cíclicas o estacionales.
El componente aleatorio mide la variabilidad de las series de tiempo después de que se retiran los otros componentes. Contabiliza la variabilidad aleatoria en una serie de tiempo ocasionada por factores imprevistos y no ocurrentes. La mayoría de los componentes irregulares se conforman de variabilidad aleatoria, si embargo, los sucesos impredecibles pueden provocar irregularidad en una variable.
Guerras, Huelgas y Desastres Naturales son ejemplos de variaciones irregulares. Estas variaciones se pueden predecir y medir pero no con certeza.
MODELO DE SERIES DE Se llama Serie de Tiempo, a un conjunto de mediciones de ciertoTIEMPO fenómeno o experimento registradas secuencialmente en el tiempo, por ejemplo a cada hora,
mensualmente, trimestralmente, semestralmente, etc.. Series de tiempo discreto, equiespaciadas en cuyo caso se asume que: {x(t1), x(t2), ..., x(tn)}= {x(1), x(2), ..., x(n)}. Debido al carácter introductorio se restringió al caso de series de tiempo univariadas. Al analizar una serie de tiempo, lo primero que se debe hacer es graficar la serie. Esto nos permite detectar las componentes esenciales de la serie. El gráfico de la serie permitirá: detectar Outlier, detectar tendencias, variación estacional, variaciones irregulares (o componente aleatoria).
Un modelo clásico para una serie de tiempo, puede ser expresada como suma o producto de tres componentes: tendencia, estacional y un término de error aleatorio. Existen tres modelos de series de tiempos. Estos son: 1.Aditivo: X(t) = T(t) + E(t) + A(t) 2.Multiplicativo: X(t) = T(t) · E(t) · A(t) 3.Mixto: X(t) = T(t) · E(t) + A(t)
Con el fin de obtener un modelo, es necesario estimar la tendencia y la estacionalidad. Para estimar la tendencia, se supone que la componente estacional no está presente. La estimación se logra al ajustar a una función de tiempo a un polinomio o suaviza miento de la serie a través de los promedios móviles. Para estimar la estacionalidad se requiere haber decidido el modelo a utilizar
APLICACIÓN Las series de tiempo se pueden citar en distintas áreas: Series económicas Series físicas Geofísica
Series de tiempo
Series demográficas Series de marketing Series de telecomunicación Series de transporte
EJEMPLOS DE LA APLICACIÓN
SERIES DE TIEMPO 1. Series económicas: 2. Series Físicas: 3. Geofísica: 4. Series demográficas: 5. Series de marketing: 6. Series telecomunicación: 7. Series de transporte:
EJEMPLOS
-
Precios de un artículo Tasas de desempleo Tasa de inflación Índice de precios, etc. Meteorología Cantidad de agua caída Temperatura máxima diaria Velocidad del viento (energía eólica) Energía solar, etc. Series sismologías
Tasas de crecimiento de la población Tasa de natalidad, mortalidad Resultados de censos poblacionales
- Series de demanda, gastos, ofertas de - Análisis de señales - Series de tráfico