Jawaban Tugas Akhir M4 Farid 5j60c
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report 3i3n4
Overview 26281t
& View Jawaban Tugas Akhir M4 Farid as PDF for free.
More details 6y5l6z
- Words: 1,154
- Pages: 7
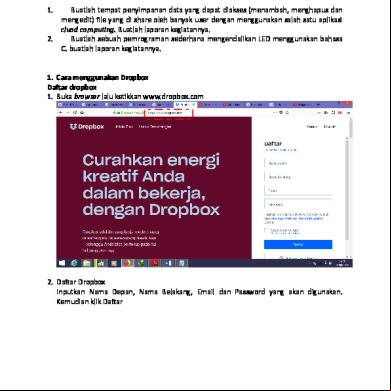
TUGAS AKHIR M4
Nama No. Peserta Prodi PPG/Kelas LPTK Tahap
: Farid Hidayat, S.Pd. : 18032118010173 : (180) Matematika / Kelas A : UNS :2
1. Buatlah bangun datar segi empat dengan diagonal-diagonalnya saling tegak lurus. Tunjukkan bahwa luas suatu segi empat yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya! Penyelesaian: Bangun datar segi empat yang diagonal-diagonalnya saling tegak lurus adalah persegi, belah ketupat dan layang.
N
D
y1 K
y A
x
x
x
x O y2
C
O
M
y
B
L
(i) belah ketupat
(ii) layang-layang D
C x O
A
B (iii) persegi
Akan dibuktian luas persegi yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: AO = OC = BO = OD = x Diagonal AC = BD = 2.AO = 2x Luas belah ketupat = 𝐿. ∆𝐴𝑂𝐵 + 𝐿. ∆𝐵𝑂𝐶 + 𝐿. ∆𝐶𝑂𝐷 + 𝐷𝑂𝐴 1
1
1
1
= 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 1
= 2 . (𝑥 2 + 𝑥 2 + 𝑥 2 + 𝑥 2 ) 1
= 2 . (4. 𝑥 2 )
1
= 2 (2𝑥). (2𝑥 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas belah ketupat = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas belah ketupat yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: BO = OD = x AO = OC = y Diagonal AC = 2.AO = 2x Diagonal BD = 2.BO = 2y Luas belah ketupat = 𝐿. ∆𝐴𝑂𝐵 + 𝐿. ∆𝐵𝑂𝐶 + 𝐿. ∆𝐶𝑂𝐷 + 𝐷𝑂𝐴 1
1
1
1
= 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 1
= 2 . (𝑥. 𝑦 + 𝑥. 𝑦 + 𝑥. 𝑦 + 𝑥. 𝑦) 1
= 2 . (4. 𝑥. 𝑦 ) 1
= 2 (2𝑥). (2𝑦 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas belah ketupat = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas layang-layang yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: KO = OM = x NO = y1 OL = y2 Diagonal KM = 2.KO = 2x Diagonal BD = NO + OL = y1 + y2 Luas layang-layang = 𝐿. ∆𝐾𝑂𝑁 + 𝐿. ∆𝑁𝑂𝑀 + 𝐿. ∆𝐾𝑂𝐿 + 𝐿. ∆𝑀𝑂𝐿 1
1
1
1
= 2 . 𝑥. 𝑦1 + 2 . 𝑥. 𝑦1 + 2 . 𝑥. 𝑦2 + 2 . 𝑥. 𝑦2 1
= 2 . (𝑥. 𝑦1 + 𝑥. 𝑦1 + 𝑥. 𝑦2 + 𝑥. 𝑦2 ) 1
= 2 . (2. 𝑥. 𝑦1 )(2. 𝑥. 𝑦2 ) 1
= 2 . 2𝑥. (𝑦1 + 𝑦2 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas layang-layang = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas segi empat sebarang yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya
Diperoleh diagonal diagonal 𝐴𝐵𝐶𝐷 adalah 𝐴𝐶 dan 𝐵𝐷 Luas segi empat 𝐴𝐵𝐶𝐷 dapat ditentukan dengan menjumlahkan luas Δ 𝐴𝐵𝐷 dan Δ 𝐵𝐶𝐷 Misal 𝐵𝐷 = 𝑝𝑎𝑛𝑗𝑎𝑛𝑔 𝑎𝑙𝑎𝑠 𝛥𝐴𝐵𝐷 = 𝑝𝑎𝑛𝑗𝑎𝑛𝑔 𝑎𝑙𝑎𝑠 𝛥𝐵𝐶𝐷, karena 𝐴𝐶 tegak lurus 𝐵𝐷 dengan titik sekitu di 𝑂 maka 𝐴𝑂 = 𝑡𝑖𝑛𝑔𝑔𝑖 𝛥𝐴𝐵𝐷 𝐶𝑂 = 𝑡𝑖𝑛𝑔𝑔𝑖 𝛥𝐵𝐶𝐷 sehingga 𝐿𝑢𝑎𝑠 𝐴𝐵𝐶𝐷 = 𝐿𝑢𝑎𝑠 𝛥𝐴𝐵𝐷 + 𝐿𝑢𝑎𝑠 𝛥𝐵𝐶𝐷 =
1 2 1
1
∙ 𝐵𝐷 ∙ 𝐴𝑂 + ∙ 𝐵𝐷 ∙ 𝐶𝑂 2
= 2 𝐵𝐷(𝐴𝑂 + 𝐶𝑂) 1
= (𝐵𝐷 ∙ 𝐴𝐶) 2
2. Lukiskan titik tembus PQ ke bidang ACF dengan P adalah titik tengah AD dan Q terletak pada BF (BQ:QF = 2:1)! Penyelesaian:
G
F
H
E
Q
S
C B D
R P
A Langkah-langkah: 1) Buatlah kubus ABCD.EFGH 2) Tentukan titik P sebagai titik tengah AD 3) Bagi garis BF menjadi 3 bagian, kemudian tentukan titik Q sehingga BQ : BF = 2:1 4) Buatlah bidang ACF 5) Tarik garis dari P ke B yang memotong AC di R 6) Tarik garis dari R ke F 7) Hubungkan P dan Q sehingga memotong garis RF di S 8) Titik S adalah titik tembus PQ ke bidang ACF
3. Tulis dalam bentuk standar, dan identifikasilah unsur-unsur (contoh: pusat, fokus, nilai a, nilai b, atau yang lainnya) yang ada pada: 𝑦 2 − 𝑥 − 𝑦 + 1 = 0, dan lukiskan grafiknya. Penyelesaian: 𝑦 2 − 𝑥 − 𝑦 + 1 = 0 merupakan persamaan parabola horizontal dengan puncak M(a, b) 𝑦2 − 𝑥 − 𝑦 + 1 = 0 1 2
1
(𝑦 2 − 2) − 4 − 𝑥 + 1 = 0 1 2
3
(𝑦 2 − 2) − 𝑥 + 4 = 0 1 2
3
(𝑦 2 − 2) = (𝑥 − 4) Dari bentuk umum persamaan parabola horizontal (𝑦 2 − 𝑏)2 = 4𝑝(𝑥 − 𝑎) diperoleh:
3 1
Titik puncak = (a, b) = (4 , 2) 1
4𝑝 = 1 ↔ 𝑝 = 4 1
3
1
1
Titik fokus = (𝑝 + 𝑎, 𝑏) = (4 + 4 , 2) = (1, 2) Persamaan garis direktris : 𝑥 = −𝑝 + 𝑎 1
3
= −4+4 1
=2 1
Sumbu simetris = 𝑦 = 𝑏 = 2 Panjang latus rectum = |4𝑝| = 1 Gambar grafik:
4. Gambarlah sebuah garis s. Pilih titik A dan B. Jika A’ pencerminan dari A, dan B’ pencerminan dari B, tunjukkan bahwa AB = A’B’! Penyelesaian: Melukis garis 𝑠 dan titik 𝐴, 𝐵, 𝐴′ , 𝐵′
Akan ditunjukkan 𝐴𝐵 = 𝐴′𝐵′ Konstruk ruas garis 𝐴𝐵, ruas garis 𝐴′𝐵′, 𝑓 = 𝑔𝑎𝑟𝑖𝑠 𝐴𝐴′, 𝑔 = 𝑔𝑎𝑟𝑖𝑠 𝐵𝐵′, ruas garis 𝐴𝐵′, ruas garis 𝐵𝐴′
𝐷 = perpotongan 𝑓 dan 𝑠 𝐶 = perpotongan 𝐴𝐵′dan 𝐵𝐴′ 𝐸 = perpotongan 𝑔 dan 𝑠 Ilustrasi ditunjukkan gambar berikut
Perhatikan 𝜟𝑩𝑪𝑫 𝒅𝒂𝒏 𝜟𝑩’𝑪𝑫 Karena 𝐵′ pencerminan 𝐵 oleh 𝑠 maka 𝑓 ⊥ 𝑠 sehingga ∠𝐵𝐶𝐷 = ∠𝐵′𝐷𝐶 𝐶𝐷 = 𝐶𝐷 (berimpit) 𝐵𝐷 = 𝐵𝐷′ (B’ pencerminan B) berdasakan teorema sisi, sudut, sisi maka 𝛥𝐵𝐶𝐷 ≅ 𝛥𝐵’𝐶𝐷
Perhatikan 𝜟𝑨𝑪𝑬 𝒅𝒂𝒏 𝜟𝑨′𝑪𝑬 Karena 𝐴′ pencerminan 𝐴 oleh 𝑠 maka g⊥ 𝑠 sehingga ∠𝐴𝐸𝐶 = ∠𝐴′𝐸𝐶 𝐸𝐶 = 𝐸𝐶 (berimpit) 𝐴𝐸 = 𝐸𝐴′ (A’ pencerminan A) berdasakan teorema sisi, sudut, sisi maka 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴′𝐶𝐸 Perhatikan ∆𝑨𝑩𝑪 dan ∆𝑨′𝑩′𝑪 Karena 𝛥𝐵𝐶𝐷 ≅ 𝛥𝐵’𝐶𝐷 maka 𝐵𝐶 = 𝐵′𝐶 Karena 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴′𝐶𝐸 maka 𝐴𝐶 = 𝐴′𝐶 Karena 𝐵𝐴′ berpotongan dengan 𝐴𝐵′ di 𝐶 maka ∠𝐴𝐶𝐵 = ∠𝐴′𝐶𝐵′ berdasakan teorema sisi, sudut, sisi maka ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶
Perhatikan ∆𝑨𝑨′𝑩′ dan ∆𝑨′𝑨𝑩 𝑨𝑨′ = 𝑨′𝑨 (berimpit) ∠𝐸𝐴′𝐶 = ∠𝐴𝐴′𝐵 (berimpit) ∠𝐸𝐴𝐶 = ∠𝐴′ 𝐴𝐵′ (berimpit) ′ Karena 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴 𝐶𝐸 maka ∠𝐸𝐴′ 𝐶 = ∠𝐸𝐴𝐶 Akibatnya ∠𝑨𝑨′ 𝑩 = ∠𝑨′𝑨𝑩′ Karena ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶 maka ∠𝐶𝐴𝐵 = ∠𝐶𝐴′𝐵′ Jelas ∠𝐴′ 𝐴𝐵 = ∠𝐸𝐴𝐶 + ∠𝐶𝐴𝐵 ∠𝐴𝐴′ 𝐵′ = ∠𝐸𝐴′ 𝐶 + ∠𝐶𝐴′ 𝐵 = ∠𝐸𝐴𝐶 + ∠𝐶𝐴𝐵 = ∠𝐴′ 𝐴𝐵 Diperoleh ∠𝐴𝐴′ 𝐵′ = ∠𝐴′ 𝐴𝐵 Berdasarkan terorema sisi, sudut, sisi ∆𝐴𝐴′𝐵′ ≅ ∆𝐴′𝐴𝐵 Akibatnya 𝐴𝐵 = 𝐴′𝐵′ Terbukti
Nama No. Peserta Prodi PPG/Kelas LPTK Tahap
: Farid Hidayat, S.Pd. : 18032118010173 : (180) Matematika / Kelas A : UNS :2
1. Buatlah bangun datar segi empat dengan diagonal-diagonalnya saling tegak lurus. Tunjukkan bahwa luas suatu segi empat yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya! Penyelesaian: Bangun datar segi empat yang diagonal-diagonalnya saling tegak lurus adalah persegi, belah ketupat dan layang.
N
D
y1 K
y A
x
x
x
x O y2
C
O
M
y
B
L
(i) belah ketupat
(ii) layang-layang D
C x O
A
B (iii) persegi
Akan dibuktian luas persegi yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: AO = OC = BO = OD = x Diagonal AC = BD = 2.AO = 2x Luas belah ketupat = 𝐿. ∆𝐴𝑂𝐵 + 𝐿. ∆𝐵𝑂𝐶 + 𝐿. ∆𝐶𝑂𝐷 + 𝐷𝑂𝐴 1
1
1
1
= 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 + 2 . 𝑥. 𝑥 1
= 2 . (𝑥 2 + 𝑥 2 + 𝑥 2 + 𝑥 2 ) 1
= 2 . (4. 𝑥 2 )
1
= 2 (2𝑥). (2𝑥 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas belah ketupat = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas belah ketupat yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: BO = OD = x AO = OC = y Diagonal AC = 2.AO = 2x Diagonal BD = 2.BO = 2y Luas belah ketupat = 𝐿. ∆𝐴𝑂𝐵 + 𝐿. ∆𝐵𝑂𝐶 + 𝐿. ∆𝐶𝑂𝐷 + 𝐷𝑂𝐴 1
1
1
1
= 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 + 2 . 𝑥. 𝑦 1
= 2 . (𝑥. 𝑦 + 𝑥. 𝑦 + 𝑥. 𝑦 + 𝑥. 𝑦) 1
= 2 . (4. 𝑥. 𝑦 ) 1
= 2 (2𝑥). (2𝑦 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas belah ketupat = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas layang-layang yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya Misal: KO = OM = x NO = y1 OL = y2 Diagonal KM = 2.KO = 2x Diagonal BD = NO + OL = y1 + y2 Luas layang-layang = 𝐿. ∆𝐾𝑂𝑁 + 𝐿. ∆𝑁𝑂𝑀 + 𝐿. ∆𝐾𝑂𝐿 + 𝐿. ∆𝑀𝑂𝐿 1
1
1
1
= 2 . 𝑥. 𝑦1 + 2 . 𝑥. 𝑦1 + 2 . 𝑥. 𝑦2 + 2 . 𝑥. 𝑦2 1
= 2 . (𝑥. 𝑦1 + 𝑥. 𝑦1 + 𝑥. 𝑦2 + 𝑥. 𝑦2 ) 1
= 2 . (2. 𝑥. 𝑦1 )(2. 𝑥. 𝑦2 ) 1
= 2 . 2𝑥. (𝑦1 + 𝑦2 ) 1
= 2 . 𝐴𝐶. 𝐵𝐷 𝟏
Luas layang-layang = 𝟐 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟏 × 𝒅𝒊𝒂𝒈𝒐𝒏𝒂𝒍 𝟐 Akan dibuktian luas segi empat sebarang yang diagonal-diagonalnya tegak lurus sesamanya sama dengan setengah perkalian diagonal-diagonalnya
Diperoleh diagonal diagonal 𝐴𝐵𝐶𝐷 adalah 𝐴𝐶 dan 𝐵𝐷 Luas segi empat 𝐴𝐵𝐶𝐷 dapat ditentukan dengan menjumlahkan luas Δ 𝐴𝐵𝐷 dan Δ 𝐵𝐶𝐷 Misal 𝐵𝐷 = 𝑝𝑎𝑛𝑗𝑎𝑛𝑔 𝑎𝑙𝑎𝑠 𝛥𝐴𝐵𝐷 = 𝑝𝑎𝑛𝑗𝑎𝑛𝑔 𝑎𝑙𝑎𝑠 𝛥𝐵𝐶𝐷, karena 𝐴𝐶 tegak lurus 𝐵𝐷 dengan titik sekitu di 𝑂 maka 𝐴𝑂 = 𝑡𝑖𝑛𝑔𝑔𝑖 𝛥𝐴𝐵𝐷 𝐶𝑂 = 𝑡𝑖𝑛𝑔𝑔𝑖 𝛥𝐵𝐶𝐷 sehingga 𝐿𝑢𝑎𝑠 𝐴𝐵𝐶𝐷 = 𝐿𝑢𝑎𝑠 𝛥𝐴𝐵𝐷 + 𝐿𝑢𝑎𝑠 𝛥𝐵𝐶𝐷 =
1 2 1
1
∙ 𝐵𝐷 ∙ 𝐴𝑂 + ∙ 𝐵𝐷 ∙ 𝐶𝑂 2
= 2 𝐵𝐷(𝐴𝑂 + 𝐶𝑂) 1
= (𝐵𝐷 ∙ 𝐴𝐶) 2
2. Lukiskan titik tembus PQ ke bidang ACF dengan P adalah titik tengah AD dan Q terletak pada BF (BQ:QF = 2:1)! Penyelesaian:
G
F
H
E
Q
S
C B D
R P
A Langkah-langkah: 1) Buatlah kubus ABCD.EFGH 2) Tentukan titik P sebagai titik tengah AD 3) Bagi garis BF menjadi 3 bagian, kemudian tentukan titik Q sehingga BQ : BF = 2:1 4) Buatlah bidang ACF 5) Tarik garis dari P ke B yang memotong AC di R 6) Tarik garis dari R ke F 7) Hubungkan P dan Q sehingga memotong garis RF di S 8) Titik S adalah titik tembus PQ ke bidang ACF
3. Tulis dalam bentuk standar, dan identifikasilah unsur-unsur (contoh: pusat, fokus, nilai a, nilai b, atau yang lainnya) yang ada pada: 𝑦 2 − 𝑥 − 𝑦 + 1 = 0, dan lukiskan grafiknya. Penyelesaian: 𝑦 2 − 𝑥 − 𝑦 + 1 = 0 merupakan persamaan parabola horizontal dengan puncak M(a, b) 𝑦2 − 𝑥 − 𝑦 + 1 = 0 1 2
1
(𝑦 2 − 2) − 4 − 𝑥 + 1 = 0 1 2
3
(𝑦 2 − 2) − 𝑥 + 4 = 0 1 2
3
(𝑦 2 − 2) = (𝑥 − 4) Dari bentuk umum persamaan parabola horizontal (𝑦 2 − 𝑏)2 = 4𝑝(𝑥 − 𝑎) diperoleh:
3 1
Titik puncak = (a, b) = (4 , 2) 1
4𝑝 = 1 ↔ 𝑝 = 4 1
3
1
1
Titik fokus = (𝑝 + 𝑎, 𝑏) = (4 + 4 , 2) = (1, 2) Persamaan garis direktris : 𝑥 = −𝑝 + 𝑎 1
3
= −4+4 1
=2 1
Sumbu simetris = 𝑦 = 𝑏 = 2 Panjang latus rectum = |4𝑝| = 1 Gambar grafik:
4. Gambarlah sebuah garis s. Pilih titik A dan B. Jika A’ pencerminan dari A, dan B’ pencerminan dari B, tunjukkan bahwa AB = A’B’! Penyelesaian: Melukis garis 𝑠 dan titik 𝐴, 𝐵, 𝐴′ , 𝐵′
Akan ditunjukkan 𝐴𝐵 = 𝐴′𝐵′ Konstruk ruas garis 𝐴𝐵, ruas garis 𝐴′𝐵′, 𝑓 = 𝑔𝑎𝑟𝑖𝑠 𝐴𝐴′, 𝑔 = 𝑔𝑎𝑟𝑖𝑠 𝐵𝐵′, ruas garis 𝐴𝐵′, ruas garis 𝐵𝐴′
𝐷 = perpotongan 𝑓 dan 𝑠 𝐶 = perpotongan 𝐴𝐵′dan 𝐵𝐴′ 𝐸 = perpotongan 𝑔 dan 𝑠 Ilustrasi ditunjukkan gambar berikut
Perhatikan 𝜟𝑩𝑪𝑫 𝒅𝒂𝒏 𝜟𝑩’𝑪𝑫 Karena 𝐵′ pencerminan 𝐵 oleh 𝑠 maka 𝑓 ⊥ 𝑠 sehingga ∠𝐵𝐶𝐷 = ∠𝐵′𝐷𝐶 𝐶𝐷 = 𝐶𝐷 (berimpit) 𝐵𝐷 = 𝐵𝐷′ (B’ pencerminan B) berdasakan teorema sisi, sudut, sisi maka 𝛥𝐵𝐶𝐷 ≅ 𝛥𝐵’𝐶𝐷
Perhatikan 𝜟𝑨𝑪𝑬 𝒅𝒂𝒏 𝜟𝑨′𝑪𝑬 Karena 𝐴′ pencerminan 𝐴 oleh 𝑠 maka g⊥ 𝑠 sehingga ∠𝐴𝐸𝐶 = ∠𝐴′𝐸𝐶 𝐸𝐶 = 𝐸𝐶 (berimpit) 𝐴𝐸 = 𝐸𝐴′ (A’ pencerminan A) berdasakan teorema sisi, sudut, sisi maka 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴′𝐶𝐸 Perhatikan ∆𝑨𝑩𝑪 dan ∆𝑨′𝑩′𝑪 Karena 𝛥𝐵𝐶𝐷 ≅ 𝛥𝐵’𝐶𝐷 maka 𝐵𝐶 = 𝐵′𝐶 Karena 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴′𝐶𝐸 maka 𝐴𝐶 = 𝐴′𝐶 Karena 𝐵𝐴′ berpotongan dengan 𝐴𝐵′ di 𝐶 maka ∠𝐴𝐶𝐵 = ∠𝐴′𝐶𝐵′ berdasakan teorema sisi, sudut, sisi maka ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶
Perhatikan ∆𝑨𝑨′𝑩′ dan ∆𝑨′𝑨𝑩 𝑨𝑨′ = 𝑨′𝑨 (berimpit) ∠𝐸𝐴′𝐶 = ∠𝐴𝐴′𝐵 (berimpit) ∠𝐸𝐴𝐶 = ∠𝐴′ 𝐴𝐵′ (berimpit) ′ Karena 𝛥𝐴𝐶𝐸 ≅ 𝛥𝐴 𝐶𝐸 maka ∠𝐸𝐴′ 𝐶 = ∠𝐸𝐴𝐶 Akibatnya ∠𝑨𝑨′ 𝑩 = ∠𝑨′𝑨𝑩′ Karena ∆𝐴𝐵𝐶 ≅ ∆𝐴′𝐵′𝐶 maka ∠𝐶𝐴𝐵 = ∠𝐶𝐴′𝐵′ Jelas ∠𝐴′ 𝐴𝐵 = ∠𝐸𝐴𝐶 + ∠𝐶𝐴𝐵 ∠𝐴𝐴′ 𝐵′ = ∠𝐸𝐴′ 𝐶 + ∠𝐶𝐴′ 𝐵 = ∠𝐸𝐴𝐶 + ∠𝐶𝐴𝐵 = ∠𝐴′ 𝐴𝐵 Diperoleh ∠𝐴𝐴′ 𝐵′ = ∠𝐴′ 𝐴𝐵 Berdasarkan terorema sisi, sudut, sisi ∆𝐴𝐴′𝐵′ ≅ ∆𝐴′𝐴𝐵 Akibatnya 𝐴𝐵 = 𝐴′𝐵′ Terbukti